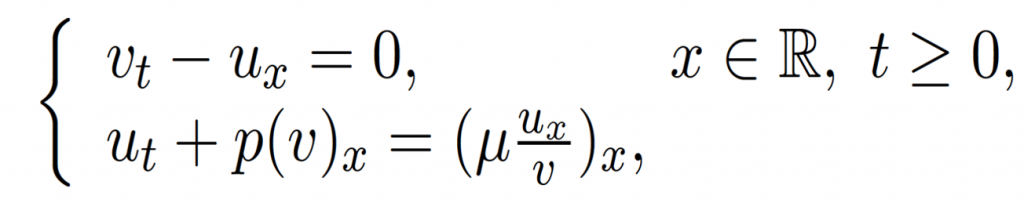We study the time-asymptotic behavior of the one-dimensional compressible barotropic Navier-Stokes system. We prove that, if initial datum is a perturbation around the superposition of rarefaction and shock, solutions approach the desired superposition as time goes on.

The compressible Navier-Stokes system is a well-known mathematical model for viscous compressible fluid dynamics. This is a viscous counterpart of the associated compressible Euler system composed of partial differential equations describing the three conservation laws of mass, momentum and energy.

The study of time-asymptotic behavior of viscous fluid flows is one of the most important topics in mathematical fluid dynamics. In particular, it remains an open problem to show that, as time goes on, solutions of the compressible Navier-Stokes system approach wave patterns that are viscous counterparts of self-similar singularities, called Riemann solutions, of the Euler system.

In the first results of this problem in 1985, Matsumura and Nishihara proved that solutions of the Navier-Stokes system converge to a viscous shock wave for the barotropic regime in one spatial dimension. In 1986, they also proved the convergence to a rarefaction wave under the same regime. However, the problem of justifying the convergence to a composite wave of shock and rarefaction has remained completely open due to the incompatibility of the anti-derivative method used for the convergence to viscous shock, and the energy method used for the convergence to rarefaction.

In collaboration with Alexis Vasseur and Yi Wang, this paper for the first time resolves the open problem under the barotropic regime in one spatial dimension. We prove that, if we consider an initial datum perturbed from a Riemann datum that generates a Riemann solution composed of rarefaction and shock, solutions approach the superposition of rarefaction and shock; especially, shock is translated by a dynamical shift. The main idea of the proof is to apply the method of a-contraction with shifts to the shock. The method of a-contraction with shifts is energy based, and so compatible with the energy method used for handling rarefaction. Combining the two methods, we seamlessly handle the superposition of waves of different kinds.

#Compressible Navier-Stokes system #Time-asymptotic behavior #Shock wave #Rarefaction wave #Superposition

Web address for full article : https://doi.org/10.1016/j.aim.2023.108963

the Name of Journal : Advances in Mathematics

Laboratory web-address of the author : https://sites.google.com/site/moonjinkang81/